A Game of Risk
This project showcases a C++ implementation of an algorithm that simulates the probability of victory in any given battle in the board game Risk. The algorithm is based on a Monte-Carlo approach, involving the efficient simulation of thousands of rounds by emulating dice rolls using repeated random draws from a probability distribution. An accurate result is calculated efficiently and almost instantaneously even for battles with thousands of dice rolls. The resulting console application was swiftly (and rightfully) banned by friends and family!
  Image Source Image Source |
|
The Rules
To provide some context on the inner workings of the algorithm, it is useful to briefly outline the rules that determine the victor in a battle in Risk. In a battle, there are a attacking units and d defending units. Battles consist of a number of rounds, until one player has no units left (or the attacker decides to stop). The possible outcomes of a round are below:
Outcomes |
| Defender loses one unit |
| Defender loses two units |
| Attacker loses one unit |
| Attacker loses two units |
| Attacker loses one unit and defender loses one unit |
In a single round, the attacking player rolls a maximum of 3 dice and the defender rolls a maximum of 2 dice. The highest dice roll of each player is compared, and then the second highest and so on. If the dice roll of the attacking player is greater than the defender’s, then the defender loses a unit. If the dice roll of the attacking player is less than or equal to the defender’s, then the attacker loses a unit. Below are some examples to demonstrate this from the official rules :
| |
Once a round has been resolved, the next round begins and new dice are cast (assuming that both players still have units left!). The attacking player can choose to stop after any round, but for our algorithm it will be assumed that the attacking player fights to the last!
Algorithm Overview
Monte carlo method
The approach that the algorithm takes is classified as a Monte Carlo method - it relies on generating random draws from a probability distribution to approximate the solution of a deterministic problem. In this instance, we are generating dice rolls to simulate battles with the given number of attacking units a and defending units d. The algorithm does this n times, to generate the probability as the proportion of battles won. As n becomes large, the estimate approaches the true probability due to the aptly named law of large numbers theory.
\[\frac{\text{number of wins}}{n} \underset{n \to \infty}{\to} \text{probability}\]Psuedocode
The basic structure of the algorithm is detailed below. Of course, the majority of the work will be done within the function calls. For more information, refer to the code breakdown section of this page or the source code itself.
Ask user for input a,d,n
Do n times:
while(a>0 and d>0):
GenerateDiceRolls()
CalculateResult()
UpdateUnitsLeft()
if a>0:
wins++
return wins/n
An alternative approach
Whilst mathematically complex, it is possible to calculate exactly the probability of a victory for any number of attackers and defenders using an analytical method. Specific details of such an approach can be found in this paper by J. A. Osbourne, with the probabilities displayed below:
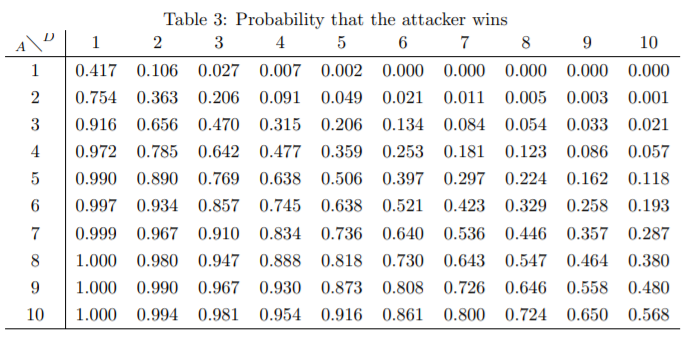 Image Source Image Source |
The most efficient program would consist of storing and retrieving these pre-calculated probabilities. Even calculating these probabilites at run-time would be more efficient than the Monte-Carlo method discussed here, particularly when the number of simulations becomes large. However, the algorithm described in this project is simpler to implement and understand, whilst still achieving an acceptable level of efficiency.
Code Breakdown
This section will break down some of the crucial parts of the algorithm’s source code, which can be found in its entirety here.
Generating Dice Rolls
Dice rolls are generated using the code below and are stored in two vectors (one for the attacker’s rolls and one for the defender’s). The size of the vectors is pre-calculated, taking into account how many dice rolls each player is currently allowed to make. This function simply iterates over the vectors and uses the rand() function from the standard template library.
//Generate random dice rolls
vector<int> aRolls(aDice);
vector<int> dRolls(dDice);
for(vector<int>::iterator it=aRolls.begin();it!=aRolls.end();it++){
*it = rand() % 6 + 1;
}
for(vector<int>::iterator it=dRolls.begin();it!=dRolls.end();it++){
*it =rand() % 6 + 1;
}
Sorting Dice Rolls
Once the dice rolls have been generated, the algorithm needs to calculate a result by comparing the dice rolls of the players. To make this convenient, the vectors are first sorted into descending order using the functions within
//Sort random dice rolls for comparison
sort(aRolls.begin(),aRolls.end());
reverse(aRolls.begin(),aRolls.end());
sort(dRolls.begin(),dRolls.end());
reverse(dRolls.begin(),dRolls.end());
Calculating the Result of a Battle Round
Since the vectors of dice rolls are already sorted, comparing the highest dice rolls of each player is a simple process. The code extract below shows this comparison and subsequent updating of (in this case a copy of) the number of units left for each player. You can also see the calculation of how many comparisons are to be made by finding the min() of the number of rolls made by each player - this allows the algorithm to handle all possible values of d and a with one function simultaneously.
//Calculate damage to attacker and defender
int battles = min(aRolls.size(),dRolls.size());
for(int i=0;i!=battles;i++){
if(aRolls[i]>dRolls[i]){
dCopy--;
}
else{
aCopy--;
}
}
Running Time Analysis
Section under construction.